题目

直接暴力的话是选择区间起点、终点、求最小值， $O(n^3)$ 的复杂度。 用 DP 可以省去重复计算最小值的部分，是 $O(n^2)$ 的复杂度，试了一下：

class Solution {
 public:
  int largestRectangleArea(vector<int>& heights) {
    size_t n = heights.size();
    vector<vector<int>> minHeight(n + 1, vector<int>(n + 1));
    int maxArea = 0;
    for (int i = 0; i < n; i++) {
      for (int j = i; j <= n; j++) {
        if (j == i) minHeight[i][i] = heights[i];
        else minHeight[i][j] = min(minHeight[i][j - 1], heights[j - 1]);
        maxArea = max(maxArea, minHeight[i][j] * (j - i));
      }
    }
    return maxArea;
  }
};

还是 TLE 了。 看了一些解答发现要用单调栈来处理，单调栈本质上是减少了需要测试的矩形的数目。

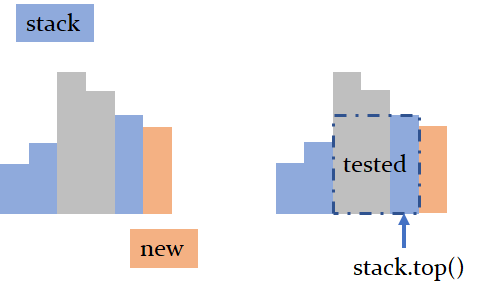
如上图所示，我们维护一个从头开始的单调栈，如果下一列比栈顶高，就入栈，矮，就出栈直到栈顶比它矮，并在出栈的同时检测矩形面积并更新最大值。

可以看出，在右边缘为橙色时，我们通过单调栈省略了左边缘为灰色的部分矩形计算，这是因为受栈顶元素影响，最小值就是栈顶元素，一步迈到栈里第二个元素 + 1 的位置就是矩形的最大长度了。

单调栈解法的时间复杂度为 $O(n)$ 。

代码